Giải SGK Toán 8 Kết nối tri thức Bài 11: Hình thang cân

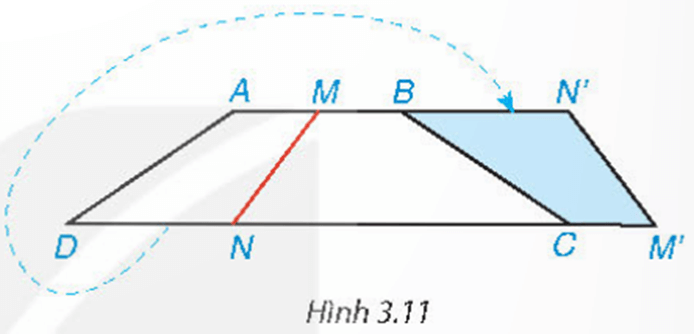
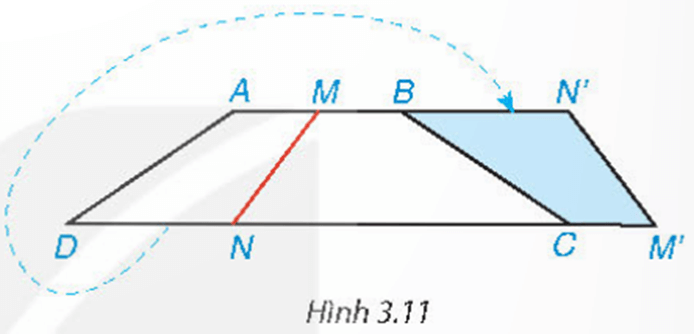
Mở đầu: Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.

Lời giải:

Ta cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy.

Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu nên ${\mathrm{AMN^\backslash widehat\{AMN\}AMN}}^{}=\widehat{M^{\prime }}$ (1)

Tứ giác ABCD là hình thang cân có AB // CD

Mà theo cách ghép thì chỗ ghép ở các đỉnh M, B tạo thành đường thẳng AN’, chỗ ghép ở các đỉnh N, C tạo thành đường thẳng DM’. Do đó AN’ // M’D.

Suy ra ${\mathrm{AMN^\backslash widehat\{AMN\}AMN}}^{}={\mathrm{MNM\prime ^\backslash widehat\{MNM\text{'}\}MNM\prime }}^{}$ (so le trong) (2)

Từ (1) và (2) suy ra ${\mathrm{MNM\prime ^\backslash widehat\{MNM\text{'}\}MNM\prime }}^{}=\widehat{M^{\prime }}$ .

Xét tứ giác MN’M’N có MN’ // M’N nên là hình thang.

Lại có ${\mathrm{MNM\prime ^\backslash widehat\{MNM\text{'}\}MNM\prime }}^{}=\widehat{M^{\prime }}$ nên MN’M’N là hình thang cân.

1. Hình thang. Hình thang cân

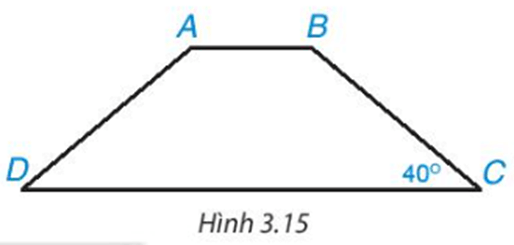
Luyện tập 1: Tính các góc của hình thang cân ABCD (AB // CD), biết $\hat{C}=40°$ (H.3.15).

Lời giải:

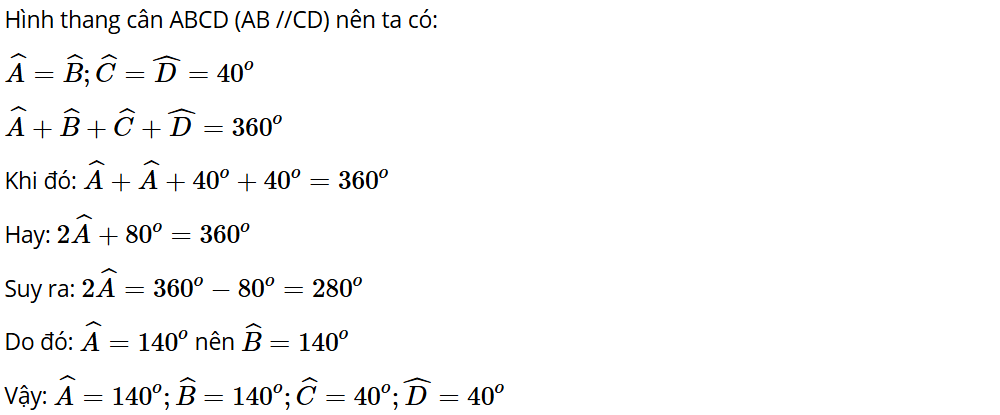
2. Tính chất của hình thang cân

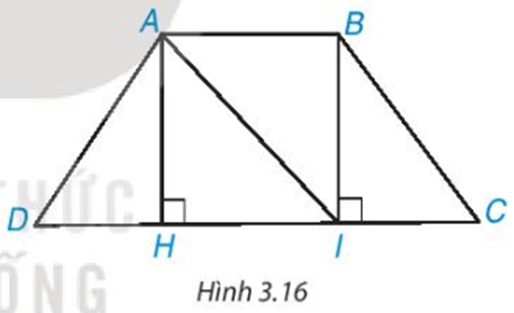
Hoạt động 1: Cho hình thang cân ABCD, AB // CD và AB < CD (H.3.16).

a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.

b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC.

Lời giải:

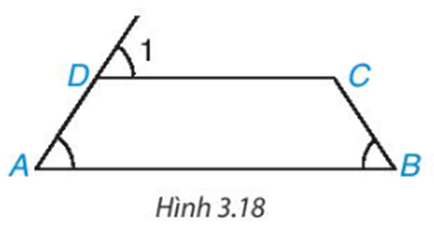
Luyện tập 2: Cho tứ giác ABCD như Hình 3.18. Biết rằng $\hat{A}=\hat{B}={\hat{D}}_1$ . Chứng minh rằng AD = BC.

Lời giải:

Ta có $\hat{A}={\hat{D}}_1$ mà hai góc này ở vị trí đồng vị nên AB // CD.

Suy ra tứ giác ABCD là hình thang.

Mặt khác hình thang ABCD có $\hat{A}=\hat{B}$ nên ABCD là hình thang cân.

Do đó AD = BC (đpcm).

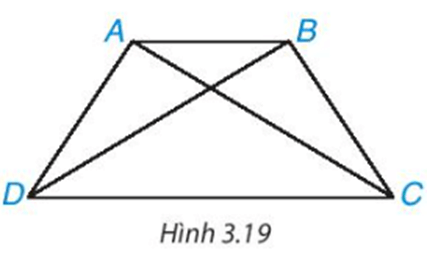
Hoạt động 2: Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ∆ACD = ∆BDC. Từ đó suy ra AC = BD.

Lời giải:

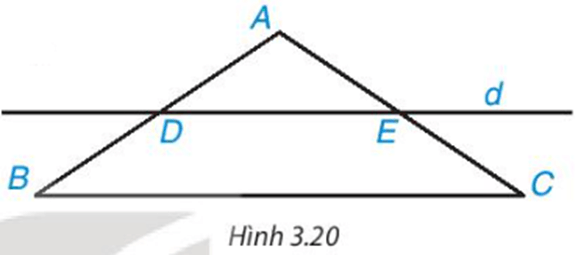
Luyện tập 3: Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).

a) Tứ giác DECB là hình gì?

b) Chứng minh BE = CD.

Lời giải:

a) Theo đề bài: d // BC nên DE // BC

Suy ra DECB là hình thang.

Vì tam giác ABC cân tại A nên $\hat{B}=\hat{C}$ .

Hình thang DECB có $\hat{B}=\hat{C}$ nên là hình thang cân.

b) Hình thang cân DECB có BE và CD là hai đường chéo.

Do đó BE = CD (đpcm).

3. Dấu hiệu nhận biết

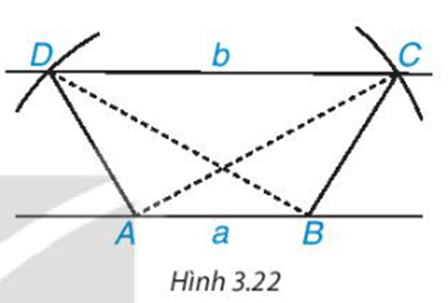
Thực hành: (H.3.22)

a) Vẽ hình thang có hai đường chéo bằng nhau theo các bước sau:

- Vẽ hai đường thẳng song song a, b. Trên a lấy hai điểm A, B.

- Vẽ hai cung tròn tâm A và B có cùng bán kính sao cho cung tròn tâm A cắt b tại C; cung tròn tâm B cắt b tại D và hai đoạn thẳng AC, BD cắt nhau. Hình thang ABCD có hai đường chéo AC và BD bằng nhau.

b) Hình thang ABCD có là hình thang cân không? Vì sao?

Lời giải:

a) Học sinh vẽ hình theo các bước đã nêu ở đề bài.

b) Hình thang ABCD có hai đường chéo AC = BD.

Do đó ABCD là hình thang cân.

Vận dụng: Hãy giải bài toán mở đầu.

Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.

Lời giải:

Ta cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy.

Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu nên ${\mathrm{AMN^AMN}}^{}=\widehat{M^{\prime }}$ (1)

Tứ giác ABCD là hình thang cân có AB // CD

Mà theo cách ghép thì chỗ ghép ở các đỉnh M, B tạo thành đường thẳng AN’, chỗ ghép ở các đỉnh N, C tạo thành đường thẳng DM’. Do đó AN’ // M’D.

Suy ra ${\mathrm{AMN^AMN}}^{}={\mathrm{MNM\prime ^MNM\prime }}^{}$ (so le trong) (2)

Từ (1) và (2) suy ra ${\mathrm{MNM\prime ^MNM\prime }}^{}=\widehat{M^{\prime }}$ .

Xét tứ giác MN’M’N có MN’ // M’N nên là hình thang.

Lại có ${\mathrm{MNM\prime ^MNM\prime }}^{}=\widehat{M^{\prime }}$ nên MN’M’N là hình thang cân.

Bài tập

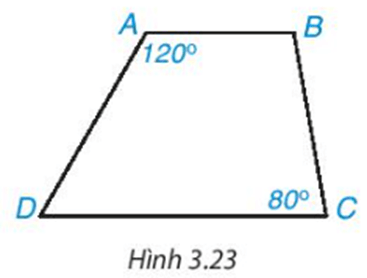
Bài 3.4: Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao?

Lời giải:

Bài 3.5: Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.

Lời giải:

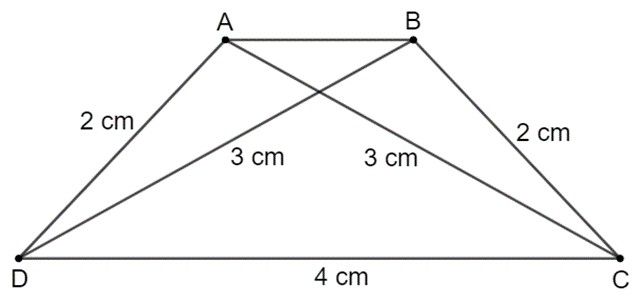
Bài 3.6: Vẽ hình thang cân ABCD (AB // CD) biết đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm.

Lời giải:

Cách vẽ hình thang cân ABCD có đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm:

– Vẽ cạnh CD = 4 cm.

– Dùng compa vẽ hai đường tròn (D; 2 cm) và (C; 3 cm). Hai đường tròn này cắt nhau tại điểm A.

– Dùng compa vẽ hai đường tròn (D; 3 cm) và (C; 2 cm). Hai đường tròn này cắt nhau tại điểm B.

– Nối AB, AD, BC ta được hình thang cân ABCD (như hình vẽ).

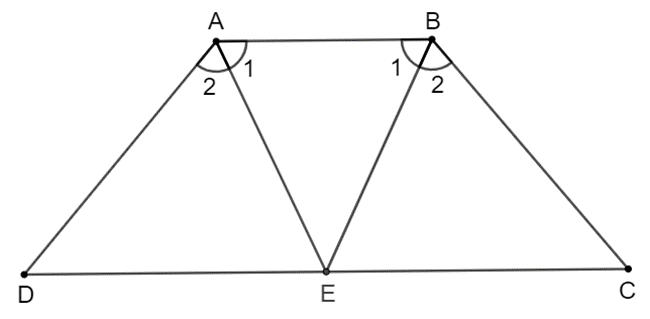
Bài 3.7: Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.

Lời giải:

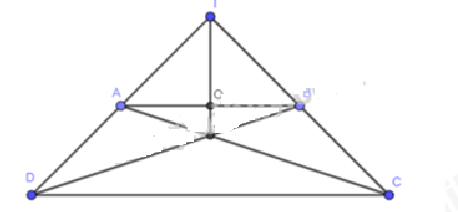
Bài 3.8: Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.

Lời giải: