Giải SGK Toán 8 Kết nối tri thức Bài 9: Phân tích đa thức thành nhân tử

Mở đầu: Tròn nói: Tớ biết cách tìm được tất cả số x để 2x2 + x = 0. Vuông thắc mắc: Tròn làm như thế nào nhỉ?

Lời giải:

Để tìm x thỏa mãn 2x2 + x = 0 thì Tròn cần phân tích đa thức 2x2 + x thành nhân tử.

Ta có: 2x2 + x = x(2x + 1) (phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung).

Khi đó x(2x + 1) = 0

x = 0 hoặc 2x + 1 = 0

x = 0 hoặc x = $\frac{-1}{2}$.

Vậy x$\in$.

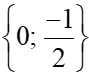
1. Phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung

Hoạt động: Hãy viết đa thức x2 – 2xy thành tích của các đa thức, khác đa thức là số.

Lời giải:

x2−2xy=x(x−2y)

Luyện tập 1: Phân tích các đa thức sau thành nhân tử:

a) 6y3 + 2y;

b) 4(x – y) – 3x(x – y).

Lời giải:

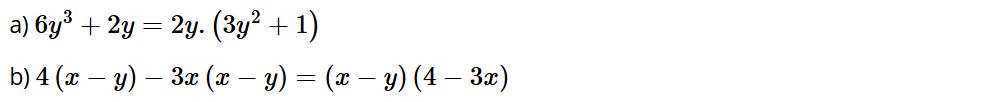
Vận dụng 1: Giải bài toán mở đầu bằng cách phân tích 2x2 + x thành nhân tử.

Lời giải:

Để tìm x thỏa mãn 2x2 + x = 0 thì Tròn cần phân tích đa thức 2x2 + x thành nhân tử.

Ta có: 2x2 + x = x(2x + 1) (phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung).

Khi đó x(2x + 1) = 0

x = 0 hoặc 2x + 1 = 0

x = 0 hoặc x = $\frac{-1}{2}$.

Vậy x$\in$.

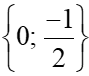
2. Phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức

Luyện tập 2: Phân tích các đa thức sau thành nhân tử:

a) (x + 1)2 – y2;

b) x3 + 3x2 + 3x + 1;

c) 8x3 – 12x2 + 6x – 1.

Lời giải:

a) (x+1)2−y2=(x+1+y)(x+1−y)

b) x3+3x2+3x+1=(x+1)3

c) 8x3−12x2+6x−1=(2x−1)3

3. Phân tích đa thức thành nhân tử bằng cách nhóm các hạng tử

Luyện tập 3: Phân tích đa thức 2x2 – 4xy + 2y – x thành nhân tử.

Lời giải:

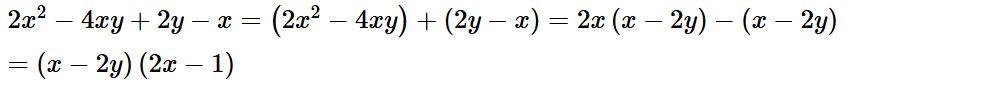
Vận dụng 2: Tính nhanh giá trị của biểu thức

A = x2 + 2y – 2x – xy tại x = 2022, y = 2020.

Lời giải:

Ta có thể phân tích đa thức A thành nhân tử theo 2 cách như sau:

Cách 1:

Ta có A = x2 + 2y – 2x – xy = (x2 – 2x) + (2y – xy)

= x(x – 2) + y(2 – x) = x(x – 2) – y(x – 2)

= (x – 2)(x – y).

Cách 2:

Ta có A = x2 + 2y – 2x – xy = (x2 – xy) – (2x – 2y)

= x(x – y) – 2(x – y) = (x – y)(x – 2).

Thay x = 2022, y = 2020 vào biểu thức A, ta được:

(2022 – 2)(2022 – 2020) = 2020 . 2 = 4040.

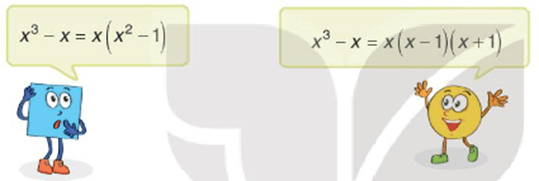
Tranh luận: Phân tích đa thức x3 – x thành nhân tử.

Em hãy nêu ý kiến của em về lời giải của Tròn và Vuông.

Lời giải:

Bài tập

Bài 2.22: Phân tích các đa thức sau thành nhân tử:

a) x2 + xy;

b) 6a2b – 18ab;

c) x3 – 4x;

d) x4 – 8x.

Lời giải:

a) x2 + xy = x(x + y);

b) 6a2b – 18ab = 6ab(a – 3);

c) x3 – 4x = x(x2 – 4) = x(x + 2)(x – 2);

d) x4 – 8x = x(x3 – 8) = x(x3 – 23)

= x(x – 2)(x2 + 2x + 22)

= x(x – 2)(x2 + 2x + 4).

Bài 2.23: Phân tích các đa thức sau thành nhân tử:

a) x2 – 9 + xy + 3y;

b) x2y + x2 + xy – 1.

Lời giải:

a) x2−9+xy+3y=(x2−9)+(xy+3y)=(x+3)(x−3)+y(x+3)=(x+3)(x−3+y)

b) x2y+x2+xy−1=(x2y+xy)+(x2−1)=xy(x+1)+(x−1)(x+1)=(x+1)(xy+x−1)

Bài 2.24: Tìm x, biết:

a) x2 – 4x = 0;

b) 2x3 – 2x = 0.

Lời giải:

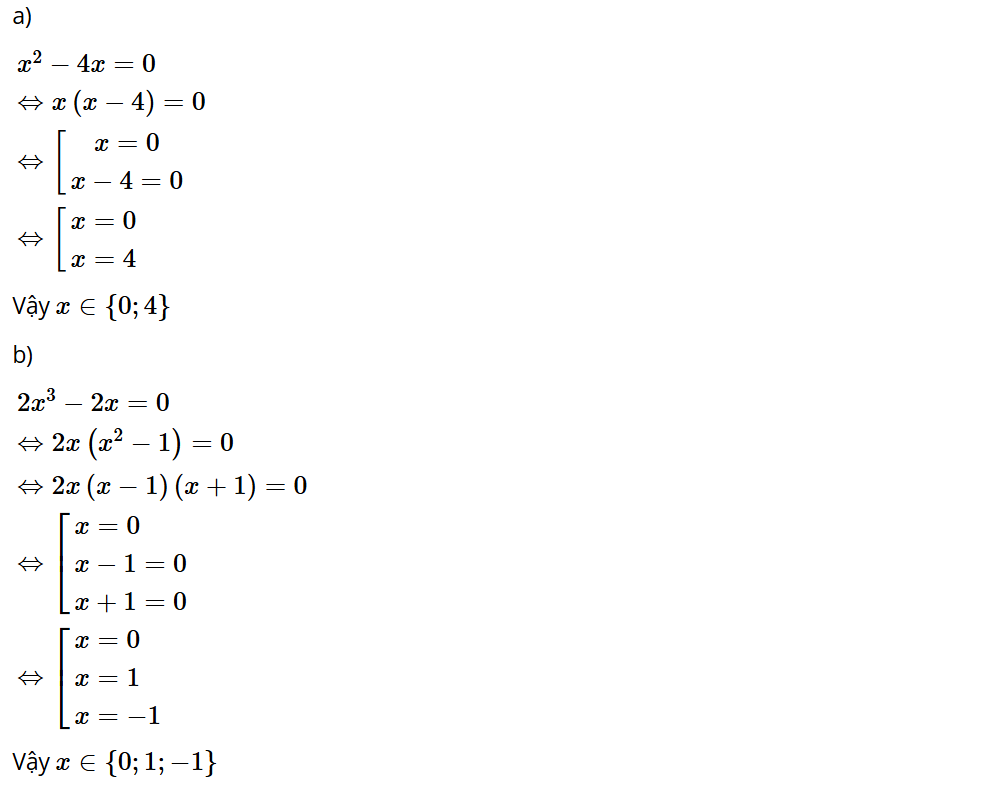
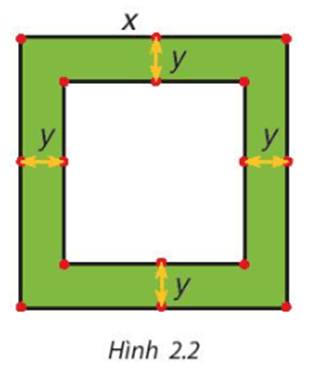
Bài 2.25: Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2).

a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.

b) Phân tích S thành nhân tử rồi tính S khi x = 102 m, y = 2 m.

Lời giải:

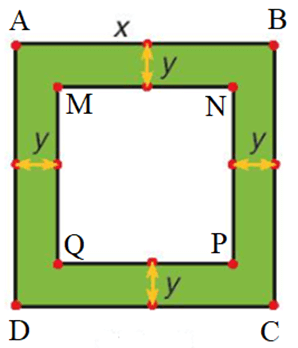
a) Đặt tên các điểm A, B, C, D, M, N, P, Q như hình vẽ.

Diện tích hình vuông ABCD là: x2 (m).

Hình vuông MNPQ có độ dài một cạnh là: x – y – y = x – 2y (m).

Diện tích hình vuông MNPQ là: (x – 2y)2 (m2).

Diện tích S của đường bao quanh mảnh vườn là:

S = x2 – (x – 2y)2 = x2 – (x2 – 4xy + 4y2)

= x2 – x2 + 4xy – 4y2 = 4xy – 4y2 (m2).

Vậy diện tích S của đường bao quanh mảnh vườn là 4xy – 4y2 (m2).

b) Phân tích đa thức S thành nhân tử, ta được:

S = 4xy – 4y2 = 4y(x – y).

Thay x = 102 m, y = 2 m vào biểu thức S, ta được:

S = 4 . 2 . (102 – 2) = 8 . 100 = 800 (m2).