Giải SGK Toán 8 Kết nối tri thức Bài 2: Đa thức - Giải SGK Toán 8 - Kết nối tri thức

1. Khái niệm đa thức

Hoạt động 1: Hãy nhớ lại, đa thức một biến là gì? Nêu một ví dụ về đa thức một biến.

Lời giải:

Đa thức một biến là tổng của những đơn thức của cùng một biến; mỗi đơn thức trong tổng đó gọi là một hạng tử của đa thức đó.

Một ví dụ về đa thức một biến: 2x3 – x2 + 1.

Hoạt động 2: Em hãy viết ra hai đơn thức tùy ý (không chứa biến, hoặc chứa từ một đến ba biến trong các biến x, y, z) rồi trao đổi với bạn ngồi cạnh để kiểm tra lại xem đã viết đúng chưa. Nếu chưa đúng, hãy cùng bạn sửa lại cho đúng.

Lời giải:

Học sinh viết ra hai đơn thức theo yêu cầu bài toán rồi trả đổi với bạn bên cạnh.

Sau đó cùng bạn sửa lại (nếu đơn thức đó viết chưa đúng).

Ví dụ: xy2;2x6

Hoạt động 3: Viết tổng của bốn đơn thức mà em và bạn ngồi cạnh đã viết.

Lời giải:

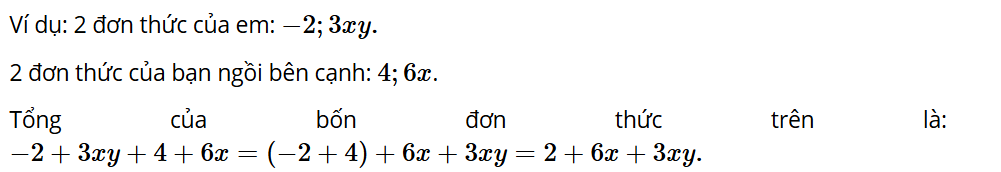
Luyện tập 1: Biểu thức nào dưới đây là đa thức? Hãy chỉ rõ các hạng tử của mỗi đa thức ấy.

$3 x y^{2} - 1; x + \frac{1}{x}; \sqrt{2} x + \sqrt{3} y; x + \sqrt{x y} + y$ .

Lời giải:

Các biểu thức là đa thức gồm: $3 x y^{2} - 1; \sqrt{2} x + \sqrt{3} y$ .

• Đa thức 3xy2 – 1 có hai hạng tử 3xy2 và – 1.

• Đa thức $\sqrt{2} x + \sqrt{3} y$ có hai hạng tử $\sqrt{2} x$ và $\sqrt{3} y$ .

Vận dụng: Mỗi quyển vở giá x đồng. Mỗi cái bút giá y đồng.

a) Viết biểu thức biểu thị số tiền phải trả để mua:

• 8 quyển vở và 7 chiếc bút;

• 3 xấp vở và 2 hộp bút, biết rằng mỗi xấp vở có 10 quyển, mỗi hộp bút có 12 chiếc.

b) Mỗi biểu thức tìm được ở câu a có phải là đa thức không?

Lời giải:

a) Giá tiền 8 quyển vở là: 8x (đồng);

Giá tiền 7 cái bút là: 7y (đồng)

Giá tiền 8 quyển vở và 7 cái bút là: 8x + 7y (đồng)

b) Mỗi xấp vở có 10 quyển nên 3 xấp vở có: 3 x 10 = 30 (quyển vở)

Giá tiền của 3 xấp vở là: 30x (đồng);

Mỗi hộp bút có 12 chiếc nên 2 hộp bút có: 12 x 2 = 24 (chiếc bút)

Giá tiền của 2 hộp bút là: 24y (đồng)

Giá tiền mua 3 xấp vở và 2 hộp bút là: 30x + 24y (đồng)

c) Hai đa thức tìm được ở hai câu trên lần lượt là: 8x + 7y; 30x + 24y đều là các đa thức.

2. Đa thức thu gọn

Câu hỏi: Đa thức nêu trong tình huống mở đầu có phải là đa thức thu gọn không?

Lời giải:

- Đa thức nêu trong tình huống mở đầu là $x^{2} + y^{2} + \frac{1}{2} x y$ là đa thức thu gọn.

Luyện tập 2: Cho đa thức $N = 5 y^{2} z^{2} - 2 x y^{2} z + \frac{1}{3} x -_{4} 2 y^{2} z^{2} + \frac{2}{3} x^{4} + x y^{2} z$ .

a) Thu gọn đa thức N.

b) Xác định hệ số và bậc của từng hạng tử (tức là bậc của từng đơn thức) trong dạng thu gọn của N.

Lời giải:

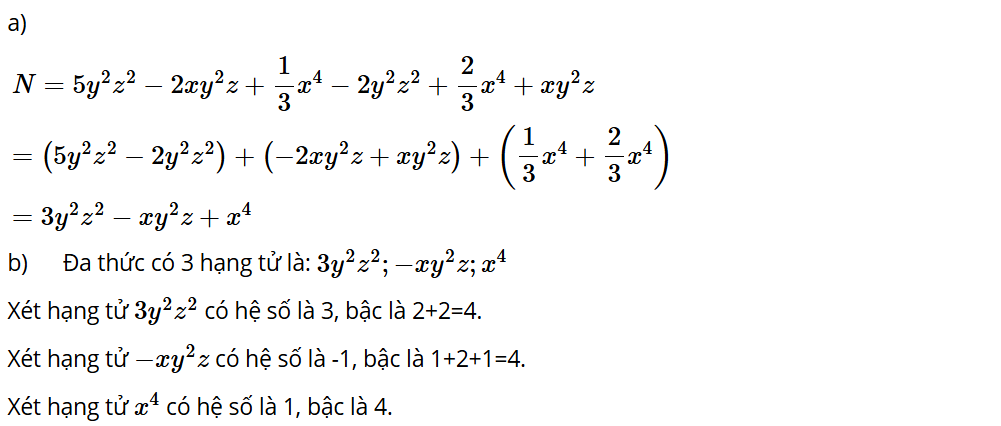
Luyện tập 3: Với mỗi đa thức sau, thu gọn (nếu cần) và tìm bậc của nó:

a) Q = 5x2 – 7xy + 2,5y2 – 8,3y + 1;

b) $H = 4 x^{5} - \frac{1}{2} x^{3} y + \frac{3}{4} x^{2} y^{2} - 4 x^{5} + 2 y^{2} - 7$ .

Lời giải:

a) Q=5x2−7xy+2,5y2+2x−8,3y+1 có bậc là 2

b) H=4x5−12x3y+34x2y2−4x5+2y2−7=−12x3y+34x2y2+2y2−7 có bậc là 4

Tranh luận: Bạn Trang nêu vấn đề: Một đa thức bậc hai thu gọn với hai biến (x và y) mà mỗi hạng tử của nó đều có hệ số bằng 1 thì có nhiều nhất là mấy hạng tử? Có ba bạn trả lời như sau:

Anh: Có 3 hạng tử.

Bình: Có 5 hạng tử.

Chung: Có 6 hạng tử.

Em hãy nêu ý kiến của mình và cho biết đó là đa thức nào.

Lời giải:

Một đa thức bậc hai thu gọn với hai biến (x và y) mà mỗi hạng tử của nó đều có hệ số bằng 1 thì có nhiều nhất là 6 hạng tử, đó là đa thức x2 + y2 + xy + x + y + 1.

Bài tập

Bài 1.8: Trong các biểu thức sau, biểu thức nào là đa thức?

−x2 + 3x + 1; $\frac{x}{\sqrt{5}}$ ; $x - \frac{\sqrt{5}}{x}$ ; 2024; 3x2y2 – 5x3y + 2,4; $\frac{1}{x^{2} + x + 1}$ .

Lời giải:

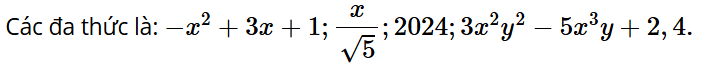
Bài 1.9: Xác định hệ số và bậc của từng hạng tử trong đa thức sau:

a) x2y – 3xy + 5x2y2 + 0,5x – 4;

b) $x \sqrt{2} - 2 x y^{3} + y^{3} - 7 x^{3} y$ .

Lời giải:

a) Đa thức x2y – 3xy + 5x2y2 + 0,5x – 4 có:

- Hạng tử x2y có hệ số là 1, bậc là 3;

- Hạng tử –3xy có hệ số là –3, bậc là 2;

- Hạng tử 5x2y2 có hệ số là 5, bậc là 4;

- Hạng tử 0,5x có hệ số là 0,5, bậc là 1;

- Hạng tử –4 có hệ số là –4, bậc là 0.

a) Đa thức $x \sqrt{2} - 2 x y^{3} + y^{3} - 7 x^{3} y$ có:

- Hạng tử $x \sqrt{2}$ có hệ số là $\sqrt{2}$ , bậc là 1;

- Hạng tử −2xy3 có hệ số là −2, bậc là 4;

- Hạng tử y3 có hệ số là 1, bậc là 3;

- Hạng tử −7x3y có hệ số là −7, bậc là 4.

Bài 1.10: Thu gọn các đa thức:

a) 5x4 – 2x3y + 20xy3 + 6x3y – 3x2y2 + xy3 – y4;

b) 0,6x3 + x2z – 2,7xy2 + 0,4x3 + 1,7xy2.

Lời giải:

a) 5x4−2x3y+20xy3+6x3y−3x2y2+xy3−y4=5x4+4x3y+21xy3−3x2y2−y4

b) 0,6x3+x2z−2,7xy2+0,4x3+1,7xy2=x3+x2z+xy2

Bài 1.11: Thu gọn (nếu cần) và tìm bậc của mỗi đa thức sau:

a) x4 – 3x2y2 + 3xy2 – x4 + 1;

b) 5x2y + 8xy – 2x2 – 5x2y + x2.

Lời giải:

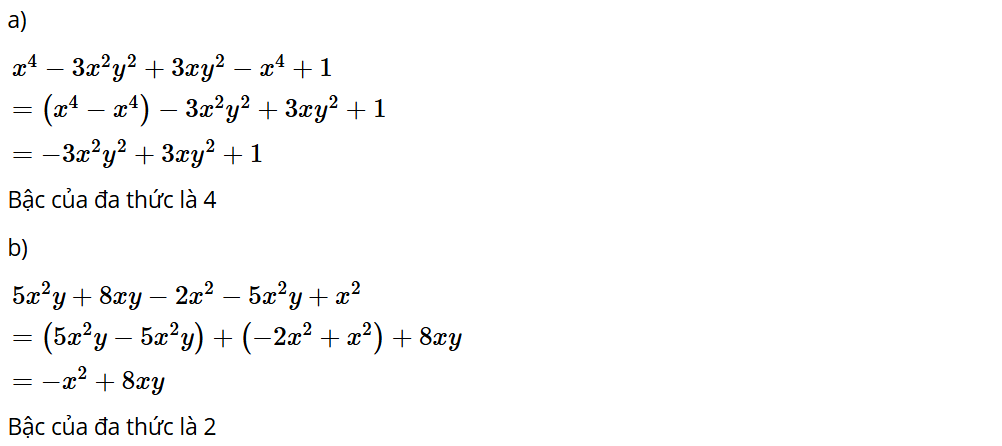
Bài 1.12: Thu gọn rồi tính giá trị của đa thức:

$M = \frac{1}{3} x^{2} y + x y^{2} - x y + \frac{1}{2} x y^{2} - 5 x y - \frac{1}{3} x^{2} y$ tại x = 0,5 và y = 1.

Lời giải:

M=13x2y+xy2−xy+12xy2−5xy−13x2y=32xy2−6xy

Thay x = 0,5 và y = 1 vào M ta có:

M=32×0,5×12−6×0,5×1=−94

Vậy M=−94 tại x = 0,5 và y = 1.

Bài 1.13: Cho đa thức P = 8x2y2z – 2xyz + 5y2z – 5x2y2z + x2y2 – 3x2y2z.

a) Thu gọn và tìm bậc của đa thức P;

b) Tính giá trị của đa thức P tại x = –4; y = 2 và z = 1.

Lời giải:

a) Ta có: P = 8x2y2z – 2xyz + 5y2z – 5x2y2z + x2y2 – 3x2y2z

= (8x2y2z – 3x2y2z– 5x2y2z) + x2y2– 2xyz + 5y2z

= x2y2 – 2xyz + 5y2z.

Hạng tử có bậc cao nhất là x2y2.

Vậy bậc của đa thức là 4.

b) Thay x = –4; y = 2 và z = 1 vào đa thức P, ta được:

P = (–4)2 . 22– 2 . (–4) . 2 . 1 + 5 . 22 . 1 = 16 . 4 + 8 . 2 + 5 . 4

= 64 + 16 + 20 = 100.

Vậy P = 100 tại x = –4; y = 2 và z = 1.