Giải SGK Toán 9 Kết nối tri thức Bài 11: Tỉ số lượng giác của góc nhọn

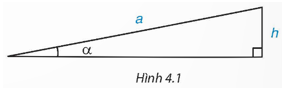
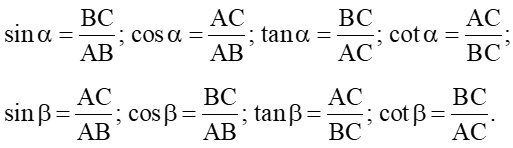Mở đầu: Ta có thể xác định “góc dốc” α của một đoạn đường dốc khi biết độ dài của dốc là a và độ cao của đỉnh dốc so với đường nằm ngang là h không? (H.4.1). (Trong các tòa chung cư, người ta thường thiết kế đoạn dốc cho người đi xe lăn với góc dốc bé hơn 6°).

Trả lời:

- Ta có thể xác định “góc dốc” α của một đoạn đường dốc khi biết độ dài của dốc là a và độ cao của đỉnh dốc so với đường nằm ngang h qua các tỉ số lượng giác của góc nhọn. Trong đó: 

1. Khái niệm tỉ số lượng giác của một góc nhọn

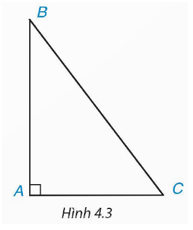
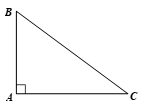
Câu hỏi: Xét góc C của tam giác ABC vuông tại A (H.4.3). Hãy chỉ ra cạnh đối và cạnh kề của góc C.

Trả lời:

- Góc C có cạnh đối là AB và cạnh kề là AC.

Hoạt động 1: Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có $\hat{B}=\widehat{B^{\prime }}=\alpha .$ Chứng minh rằng:

a) ∆ABC ᔕ ∆A’B’C’;

b) $\frac{AC}{BC}=\frac{A^{\prime }{C}^{\prime }}{B^{\prime }{C}^{\prime }};\frac{AB}{BC}=\frac{A^{\prime }{B}^{\prime }}{B^{\prime }{C}^{\prime }};\frac{AC}{AB}=\frac{A^{\prime }{C}^{\prime }}{A^{\prime }{B}^{\prime }};\frac{AB}{AC}=\frac{A^{\prime }{B}^{\prime }}{A^{\prime }{C}^{\prime }}.$

Trả lời:

Luyện tập 1: Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B.

Trả lời:

Theo định lý Pythagore, ta có: BC2 = AB2 + AC2 = 52 + 122 = 169 nên BC = 13 cm

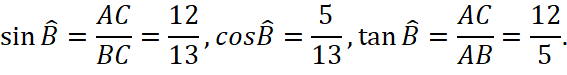
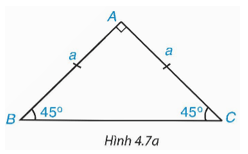
Hoạt động 2: Cho tam giác ABC vuông cân tại A và AB = AC = a (H.4.7a).

a) Hãy tính BC và các tỉ số $\frac{AB}{BC},\frac{AC}{BC}.$ Từ đó suy ra sin45°, cos45°.

b) Hãy tính các tỉ số $\frac{AB}{AC}$và $\frac{AC}{AB}.$Từ đó suy ra tan45°, cot45°.

Trả lời:

Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:

BC2 = AB2 + AC2 = a2 + a2 = 2a2, suy ra $BC=\sqrt{2a^2}=a\sqrt{2}$(cm).

∆ABC vuông tại A có AB = AC nên ∆ABC vuông cân tại A nên $\hat{B}=\hat{C}=45°.$

a) Ta có: $\frac{AB}{BC}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$ và $\frac{AC}{BC}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}.$

Do đó $\sin 45°=\sin B=\frac{AC}{BC}=\frac{\sqrt{2}}{2};$ $\cos 45°=\cos B=\frac{AB}{BC}=\frac{\sqrt{2}}{2}.$

b) Ta có: $\frac{AB}{AC}=\frac{a}{a}=1;\frac{AC}{AB}=\frac{a}{a}=1.$

Do đó $\tan 45°=\tan B=\frac{AC}{AB}=1;\cot 45°=\cot B=\frac{AB}{AC}=1.$

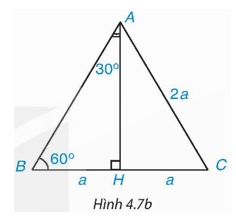
Hoạt động 3: Xét tam giác đều ABC có cạnh bằng 2a.

a) Tính đường cao AH của tam giác ABC (H.4.7b).

b) Tính sin30°, cos30°, sin60° và cos60°.

c) Tính tan30°, cot30°, tan60° và cot60°.

Trả lời:

 a) Theo định lí Pythagore ta có: AH2 = AB2 – BH2 = (2a)2 – a2 = 3a2

=> AH = .

b) Ta có: 

c) Ta có: 

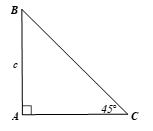
Luyện tập 2: Cho tam giác ABC vuông tại A có $\hat{C}=45°$ và AB = c. Tính BC và AC theo c.

Trả lời:

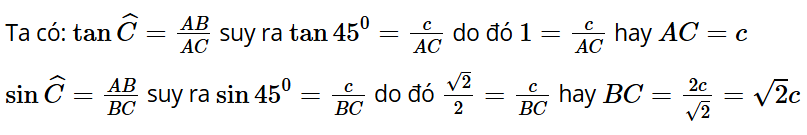
2. Tỉ số lượng giác của hai góc phụ nhau

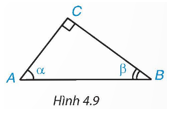
Hoạt động 4: Cho tam giác ABC vuông tại C, có $\hat{A}=\alpha ,\hat{B}=\beta$ (H.4.9). Hãy viết các tỉ số lượng giác của góc α, β theo độ dài các cạnh của tam giác ABC. Trong các tỉ số đó, cho biết các cặp tỉ số bằng nhau.

Trả lời:

Xét ∆ABC vuông tại C, theo định nghĩa tỉ số lượng giác, ta có:

Từ đó ta có: sin α = cos β; cosα = sin β; tanα = cos β; cot α = tan β.

Luyện tập 3: Hãy giải thích tại sao sin35° = cos55°, tan35° = cot55°.

Trả lời:

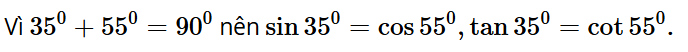
3. Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn

Luyện tập 4: Sử dụng MTCT tính các tỉ số lượng giác và làm tròn kết quả đến chữ số thập phân thứ ba:

a) sin40°54’;

b) cos52°15’;

c) tan69°36’;

d) cot25°18’.

Trả lời:

a) sin 40o54’ = 0,655             b) cos 52o15’ = 0,612

c) tan 69o36’ = 2,689             d) cot 25o18’ = 2,116.

Luyện tập 5: Dùng MTCT, tìm các góc α (làm tròn đến phút), biết:

a) sinα = 0,3782;

b) cosα = 0,6251;

c) tanα = 2,154;

d) cotα = 3,253.

Trả lời:

Vận dụng: Trở lại bài toán ở tình huống mở đầu. Trong một tòa chung cư, biết đoạn dốc vào sảnh tòa nhà dài 4 m, độ cao của đỉnh dốc bằng 0,4 m.

a) Hãy tính góc dốc.

b) Hỏi góc đó có đúng tiêu chuẩn của dốc cho người đi xe lăn không?

Trả lời:

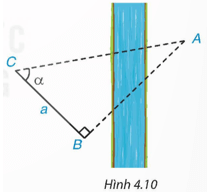
Tranh luận: Để tính khoảng cách giữa hai địa điểm A, B không đo trực tiếp được, chẳng hạn A và B là hai địa điểm ở hai bên sông, người ta lấy điểm C về phía bờ sông có chứa B sao cho tam giác ABC vuông tại B. Ở bên bờ sông chứa B, người ta đo được ${\mathrm{ACB^\backslash widehat\{ACB\}ACB}}^{}=\alpha$ và BC = a (H.4.10). Với các dữ liệu đó, đã tính được khoảng cách AB chưa? Nếu được, hãy tính AB, biết α = 55°, a = 70 m.

Vuông cho rằng: Không thể tính được AB vì trong tam giác vuông ABC, theo định lí Pythagore, phải biết được hai cạnh mới tính được cạnh thứ ba. Tròn khẳng định: Với các dữ liệu đã biết là có thể tính được khoảng cách AB rồi. Em hãy cho biết ý kiến của mình.

Trả lời:

Có thể tính được AB, dựa trên công thức 

Khi α = 55o, a = 70 m thì 

Bài tập

Bài 4.1: Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, coossin, tang, cotang của các góc nhọn B và C khi biết:

a) AB = 8 cm, BC = 17 cm;

b) AC = 0,9 cm, AB = 1,2 cm.

Trả lời:

a) Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:

BC2 = AB2 + AC2

Suy ra AC2 = BC2 – AB2 = 172 – 82 = 225.

Do đó AC = 15 cm.

Xét ∆ABC vuông tại A, theo định nghĩa tỉ số lượng giác sin, côsin, tang, cotang và định lí tỉ số lượng giác của hai góc phụ nhau, ta có:

● $\sin B=\cos C=\frac{AC}{BC}=\frac{15}{17};$

● $\cos B=\sin C=\frac{AB}{BC}=\frac{8}{17};$

● $\tan B=\cot C=\frac{AC}{AB}=\frac{15}{8};$

● $\cot B=\tan C=\frac{AB}{AC}=\frac{8}{15}.$

b) Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:

BC2 = AB2 + AC2 = 1,22 + 0,92 = 2,25

Do đó BC = 1,5 cm.

Xét ∆ABC vuông tại A, theo định nghĩa tỉ số lượng giác sin, côsin, tang, cotang và định lí tỉ số lượng giác của hai góc phụ nhau, ta có:

● $\sin B=\cos C=\frac{AC}{BC}=\frac{\mathrm{0,9}}{\mathrm{1,5}}=\frac{3}{5};$

● $\cos B=\sin C=\frac{AB}{BC}=\frac{\mathrm{1,2}}{\mathrm{1,5}}=\frac{4}{5};$

● $\tan B=\cot C=\frac{AC}{AB}=\frac{\mathrm{0,9}}{\mathrm{1,2}}=\frac{3}{4};$

● $\cot B=\tan C=\frac{AB}{AC}=\frac{\mathrm{1,2}}{\mathrm{0,9}}=\frac{4}{3}.$

Bài 4.2: Cho tam giác vuông có một góc nhọn 60° và cạnh kề với góc 60° bằng 3 cm. Hãy tính cạnh đối của góc này.

Trả lời:

Ta có: tan 60o =  mà tan 60o =

Độ dài cạnh kề là: .

Bài 4.3: Cho tam giác vuông có một góc nhọn bằng 30° và cạnh đối với góc này bằng 5 cm. Tính độ dài cạnh huyền của tam giác.

Trả lời:

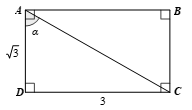
Bài 4.4: Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và √3. Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác trang 69).

Trả lời:

Gọi hình chữ nhật trong bài là hình chữ nhật ABCD với chiều rộng là cạnh $AD=\sqrt{3},$ chiều dài là cạnh CD = 3, đường chéo AC, góc tạo bởi đường chéo và cạnh ngắn hơn của hình chữ nhật là góc α.

Xét ∆ABC vuông tại D, theo định nghĩa tỉ số lượng giác tan, ta có:

$\tan \alpha =\frac{CD}{AD}=\frac{3}{\sqrt{3}}=\sqrt{3},$ suy ra α = 60°.

Vậy góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật đã cho là 60°.

Bài 4.5:

a) Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45°:

sin55°, cos62°, tan57°, cot64°.

b) Tính $\frac{\tan 25°}{\cot 65°},\tan 34°-\cot 56°.$

Trả lời:

a) sin 55o = cos 45o, cos 62o = sin 28o, tan 57o = cot 33o, cot 64o = tan 26o.

b) Ta có:  (do 65o và 25o là hai góc phụ nhau)

 (do 34o và 56o là hai góc phụ nhau)

Bài 4.6: Dùng MTCT, tính (làm tròn đến chữ số thập phân thứ ba):

a) sin40°12’;

b) cos52°54’;

c) tan63°36’;

d) cot35°20’.

Trả lời:

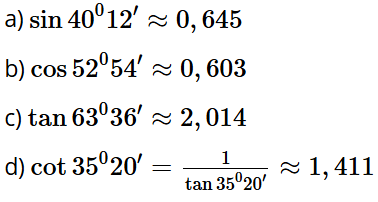
Bài 4.7: Dùng MTCT, tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng:

a) sinx = 0,2368;

b) cosx = 0,6224;

c) tanx = 1,236;

d) cotx = 2,154.

Trả lời: