Giải SGK Toán 9 Kết nối tri thức Luyện tập chung

Bài 2.12: Giải các phương trình sau:

a) 2(x + 1) = (5x – 1)(x + 1);

b) (–4x + 3)x = (2x + 5)x.

Trả lời:

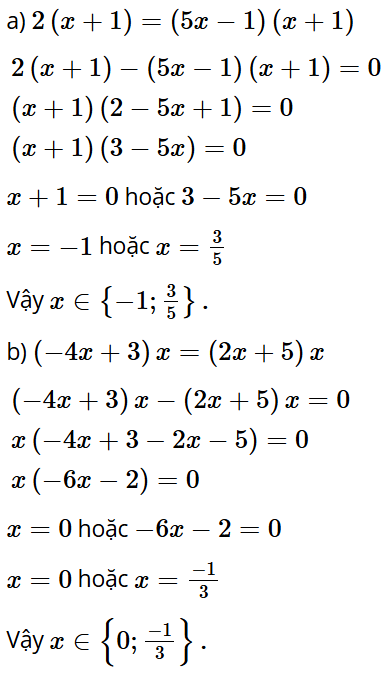
Bài 2.13: Để loại bỏ x% một loại tảo độc khỏi một hồ nước, người ta ước tính chi phí cần bỏ ra là

$C\left(x\right)=\frac{50x}{100-x}$(triệu đồng), với 0 ≤ x < 100.

Nếu bỏ ra 450 triệu đồng, người ta có thể loại bỏ được bao nhiêu phần trăm loại tảo độc đó?

Trả lời:

Nếu bỏ ra 450 triệu đồng (tức C(x) = 450), khi đó ta có:

50x = 450(100-x)

50x = 45000 – 450x

50x + 450x = 45000

500x = 45000

x = 90

Vậy nếu bỏ ra 450 triệu đồng, người ta có thể loại bỏ được 90% loại tảo độc đó.

Bài 2.14: Giải các phương trình sau:

a) $\frac{1}{x+2}-\frac{2}{x^2-2x+4}=\frac{x-4}{x^3+8};$

b) $\frac{2x}{x-4}+\frac{3}{x+4}=\frac{x-12}{x^2-16}.$

Trả lời:

a) $\frac{1}{x+2}-\frac{2}{x^2-2x+4}=\frac{x-4}{x^3+8}$

ĐKXĐ: x ≠ –2.

Quy đồng mẫu hai vế của phương trình, ta được:

$\frac{x^2-2x+4-2\left(x+2\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{x-4}{\left(x+2\right)\left(x^2-2x+4\right)}$

$\frac{x^2-4x}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{x-4}{\left(x+2\right)\left(x^2-2x+4\right)}.$

Suy ra x2 – 4x = x – 4. (*)

Giải phương trình (*):

x2 – 4x = x – 4

x(x – 4) – (x – 4) = 0

(x – 4)(x – 1) = 0

x – 4 = 0 hoặc x – 1 = 0

x = 4 (thỏa mãn ĐKXĐ) hoặc x = 1 (thỏa mãn ĐKXĐ).

Vậy phương trình đã cho có nghiệm là x = 4 và x = 1.

b) $\frac{2x}{x-4}+\frac{3}{x+4}=\frac{x-12}{x^2-16}$

ĐKXĐ: x ≠ 4 và x ≠ –4.

Quy đồng mẫu hai vế của phương trình:

$\frac{2x\left(x+4\right)+3\left(x-4\right)}{\left(x-4\right)\left(x+4\right)}=\frac{x-12}{\left(x-4\right)\left(x+4\right)}$

$\frac{2x^2+11x-12}{\left(x-4\right)\left(x+4\right)}=\frac{x-12}{\left(x-4\right)\left(x+4\right)}.$

Suy ra 2x2 + 11x – 12 = x – 12. (*)

Giải phương trình (*):

2x2 + 11x – 12 = x – 12

2x2 + 11x – 12 – x + 12 = 0

2x2 + 10x = 0

2x(x + 5) = 0

2x = 0 hoặc x + 5 = 0

x = 0 (thỏa mãn ĐKXĐ) hoặc x = –5 (thỏa mãn ĐKXĐ).

Vậy phương trình đã cho có nghiệm là x = 0 và x = –5.

Bài 2.15: Cho a > b, chứng minh rằng:

a) 4a + 4 > 4b + 3;

b) 1 – 3a < 3 – 3b.

Trả lời: