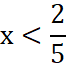Giải SGK Toán 9 Kết nối tri thức Bài tập cuối chương II

A. Trắc nghiệm

Bài 2.21: Nghiệm của bất phương trình –2x + 1 < 0 là

A. $x<\frac{1}{2}.$

B. $x>\frac{1}{2}.$

C. $x\le \frac{1}{2}.$

D. $x\ge \frac{1}{2}.$

Đáp án: B

Giải thích:

Ta có:

–2x + 1 < 0

–2x < –1

$x>\frac{1}{2}.$

Vậy nghiệm của bất phương trình –2x + 1 < 0 là $x>\frac{1}{2}.$

Bài 2.22: Điều kiện xác định của phương trình $\frac{x}{2x+1}+\frac{3}{x-5}=\frac{x}{\left(2x+1\right)\left(x-5\right)}$ là

A. $x\ne -\frac{1}{2}.$

B. $x\ne -\frac{1}{2}$ và x ≠ –5.

C. x ≠ 5.

D. $x\ne -\frac{1}{2}$ và x ≠ 5.

Đáp án: D

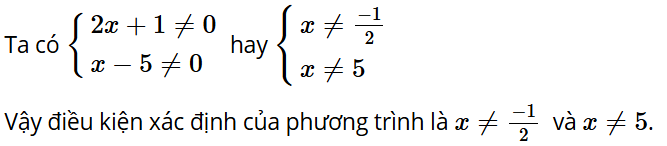
Bài 2.23: Phương trình x – 1 = m + 4 có nghiệm lớn hơn 1 với

A. m ≥ –4.

B. m ≤ 4.

C. m > –4.

D. m < –4.

Đáp án: C

Giải thích:

Từ x – 1 = m + 4, suy ra x = m + 5.

Theo bài, phương trình x – 1 = m + 4 có nghiệm lớn hơn 1 nên ta có: x > 1.

Suy ra m + 5 >1, do đó m > –4.

Bài 2.24: Nghiệm của bất phương trình 1 – 2x ≥ 2 – x là

A. $x>\frac{1}{2}.$

B. $x<\frac{1}{2}.$

C. x ≤ –1.

D. x ≥ –1.

Đáp án: C

Giải thích:

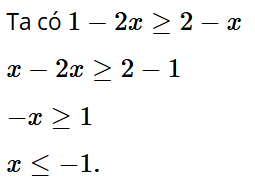
Bài 2.25: Cho a > b. Khi đó ta có:

A. 2a > 3b.

B. 2a > 2b + 1.

C. 5a + 1 > 5b + 1.

D. –3a < –3b – 3.

Đáp án: C

Giải thích:

Ta có: a >  b, suy ra 5a > 5b, do đó 5a + 1 > 5b + 1.

Vậy ta chọn phương án C.

B. Tự luận

Bài 2.26: Giải các phương trình sau:

a) (3x – 1)2 – (x + 2)2 = 0;

b) x(x + 1) = 2(x2 – 1).

Trả lời:

a)

(3x – 1 + x + 2)(3x – 1 – x – 2) = 0

(4x + 1)(2x – 3) = 0

Vậy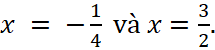

b)

x(x+1)=2(x-1)(x+1).

x(x+1)-2(x-1)(x+1)=0

x(x+1)-(2x-2).(x+1)

(x+1)(x – 2x + 2)=0

(x+1)(-x + 2) =0

Vậy x = -1 và x = 2.

Bài 2.27: Giải các phương trình sau:

a) $\frac{x}{x-5}-\frac{2}{x+5}=\frac{x^2}{x^2-25};$

b) $\frac{1}{x+1}-\frac{x}{x^2-x+1}=\frac{3}{x^3+1}.$

Trả lời:

Bài 2.28: Cho a < b, hãy so sánh:

a) a + b + 5 với 2b + 5;

b) –2a – 3 với – (a + b) – 3.

Trả lời:

a) Do a < b, nên a + b < b + b hay a + b < 2b.

Suy ra a + b + 5 < 2b + 5.

Vậy a + b + 5 < 2b + 5.

b) Do a < b, nên a + a < a + b hay 2a < a + b.

Suy ra –2a > –(a + b), do đó –2a – 3> – (a + b) – 3.

Vậy –2a – 3 > – (a + b) – 3.

Bài 2.29: Giải các bất phương trình:

a) 2x + 3(x + 1) > 5x – (2x – 4);

b) (x + 1)(2x – 1) < 2x2 – 4x + 1.

Trả lời:

a) 2x + 3(x + 1) > 5x – (2x – 4)

2x + 3x + 3 > 5x – 2x  + 4

5x + 3 > 3x + 4

2x > 1

b) 

5x < 2