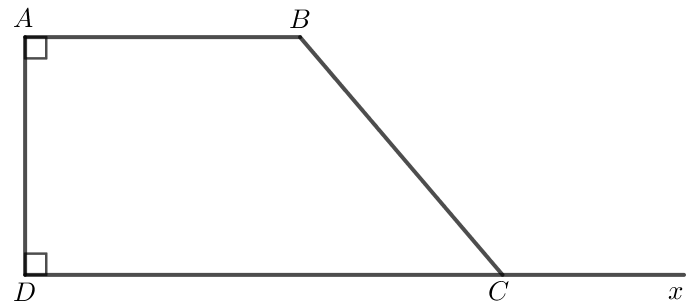
Bài 3.27: Cho hình thang ABCD có cạnh AD vuông góc với hai đáy AB và CD. Số đo góc ở đỉnh B gấp đôi số đo góc ở đỉnh C. Tính số đo các góc của hình thang đó.
Lời giải:
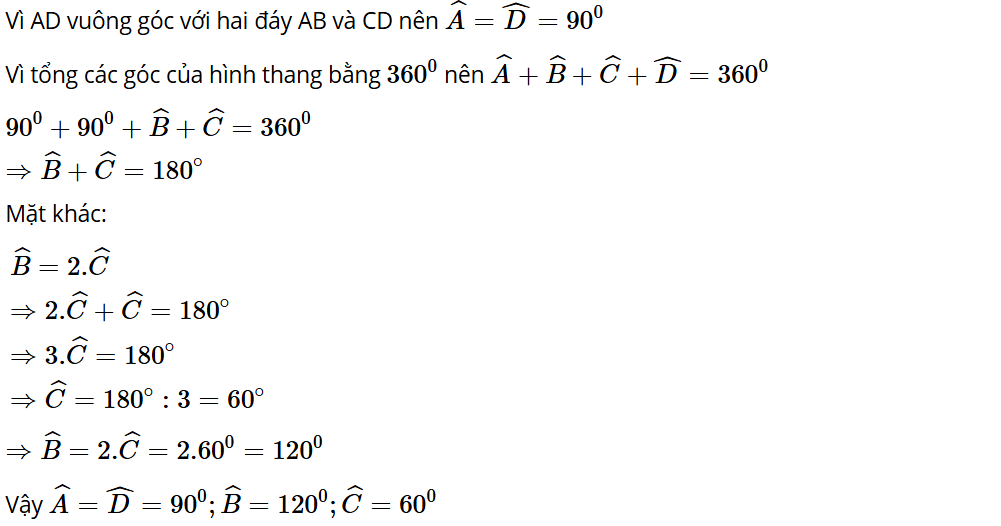
Bài 3.28: Vẽ hình minh họa và viết giả thiết, kết luận của định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”.
Lời giải:
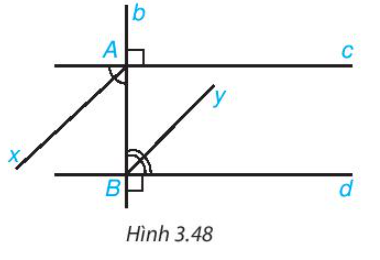
Bài 3.29: Kẻ các tia phân giác Ax, By của một cặp góc so le trong tạo bởi đường thẳng b vuông góc với hai đường thẳng song song c, d (H.3.48). Chứng minh rằng hai tia phân giác đó nằm trên hai đường thẳng song song.
Lời giải:
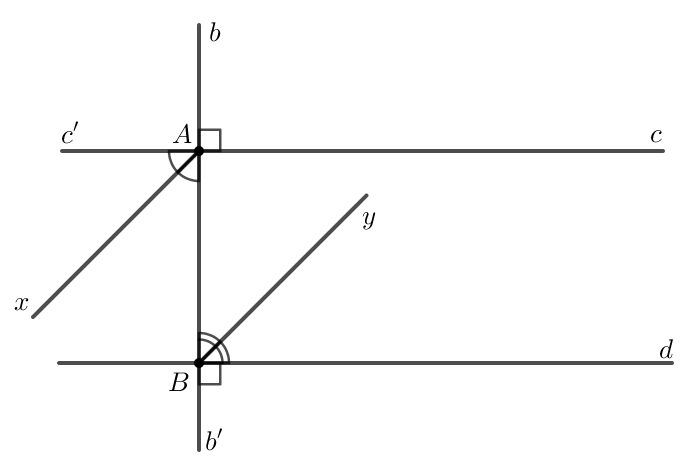
- Vì Ax là tia phân giác của góc vuông A nên
- Vì By là tia phân giác của góc B vuông nên
=>
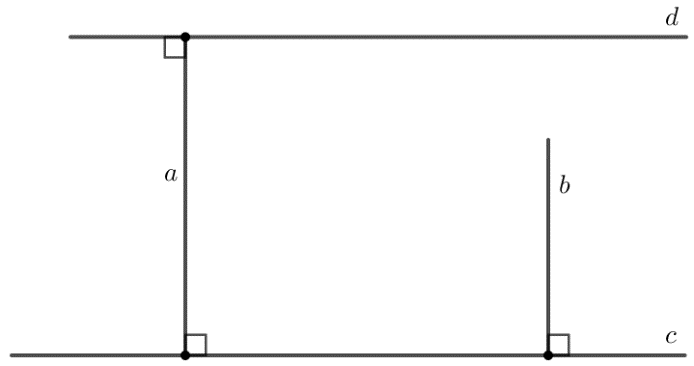
Bài 3.30: Cho hai đường thẳng phân biệt a, b cùng vuông góc với đường thẳng c; d là một đường thẳng khác c và d vuông góc với a. Chứng minh rằng:
a) a // b;
b) c // d;
c)
Lời giải:
a) Áp dụng định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” ta có:
Do nên a // b.
Vậy a // b.
b) Áp dụng định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” ta có:
Do nên c // d.
Vậy c // d.
c) Áp dụng định lí: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại” ta có:
Do nên
Vậy
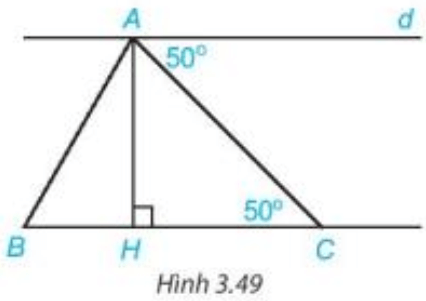
Bài 3.31: Cho Hình 3.49.
Chứng minh rằng:
a) d // BC;
b)
c) Trong các kết luận trên, kết luận nào được suy ra từ tính chất của hai đường thẳng song song, kết luận nào được suy ra từ dấu hiệu nhận biết hai đường thẳng song song?
Lời giải: