Giải SGK Toán 7 Kết nối tri thức Luyện tập chung (trang 85, 86)

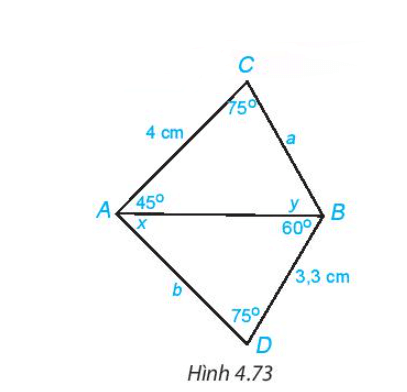
Bài 4.29: Cho Hình 4.73. Hãy tìm số đo x, y của các góc và độ dài a, b của các đoạn thẳng trên hình vẽ.

Lời giải:

Xét tam giác ABC có ${\mathrm{BAC^\backslash widehat\{BAC\}BAC}}^{}+{\mathrm{ABC^\backslash widehat\{ABC\}ABC}}^{}+{\mathrm{BCA^\backslash widehat\{BCA\}BCA}}^{}=180°.$

Do đó $\widehat{ABC}=180°-{\mathrm{BAC^\backslash widehat\{BAC\}BAC}}^{}-{\mathrm{BCA^\backslash widehat\{BCA\}BCA}}^{}$ hay $y=180°-45°-75°=60°.$

Xét tam giác ABD có ${\mathrm{XA^ˊU^\backslash widehat\{XẤU\}}}^{}BA^\backslash widehat\{BA\}BAD +ABD^\backslash widehat\{ABD\}ABD+{\mathrm{BDA^\backslash widehat\{BDA\}BDA}}^{}=180°.$

Do đó ${\mathrm{BA^\backslash widehat\{BA\}BAD}}^{}=180°-{\mathrm{ABD^\backslash widehat\{ABD\}ABD}}^{}-{\mathrm{BDA^\backslash widehat\{BDA\}BDA}}^{}$ hay $x=180°-60°-75°=45°.$

Xét hai tam giác ABC và ABD có:

${\mathrm{DAB^\backslash widehat\{DAB\}CAB}}^{}={\mathrm{DAB^\backslash widehat\{DAB\}DAB}}^{}$ (cùng bằng 45o).

AB chung.

${\mathrm{ABC^\backslash widehat\{ABC\}ABC}}^{}={\mathrm{ABD^\backslash widehat\{ABD\}ABD}}^{}$ (cùng bằng 60o).

Do đó $\Delta ABC=\Delta AB\text{D}$ (g – c – g).

Khi đó BC = BD = 3,3 cm (2 cạnh tương ứng), AC = AD = 4 cm (2 cạnh tương ứng).

hay a = 3,3 cm; b = 4 cm.

Vậy $x=45°;y=60°;$ a = 3,3 cm; b = 4 cm.

Bài 4.30: Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM. Chứng minh rằng:

a) $\Delta OAN=\Delta OBM;$

b) $\Delta AMN=\Delta BNM.$

Lời giải:

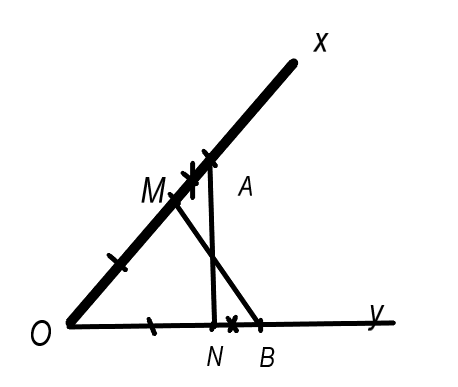
a. Xét ΔOAN và ΔOBM, ta có :

• OA= OB
• Góc O chung
• OM= ON

=> ΔOAN = ΔOBM (c-g-c)

b. Từ câu a => AN= BM. Mà OA = OB=> AM =BN

Xét ΔAMN và ΔBNM, ta có :

• AN= BM
• AM =BN
• MN chung

=> ΔAMN = ΔBNM (c-c-c)

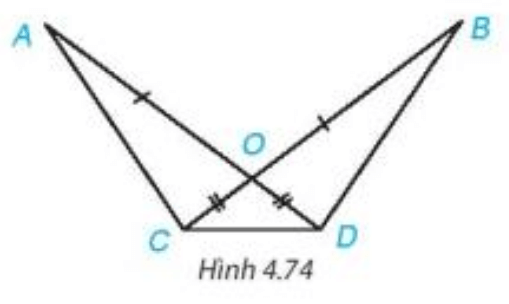
Bài 4.31: Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:

a) AC = BD;

b) $\Delta AC\text{D}=\Delta B\text{D}C.$

Lời giải:

Bài 4.32: Cho tam giác MBC vuông tại M có $\hat{B}=60°.$ Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.

Lời giải:

Xét hai tam giác AMC vuông tại M và BMC vuông tại M có:

AM = BM (theo giả thiết).

MC chung.

Do đó $\Delta AMC=\Delta BMC$ (2 cạnh góc vuông).

Khi đó AC = BC (2 cạnh tương ứng).

Tam giác ABC có AC = BC nên tam giác ABC cân tại C.

Tam giác ABC cân tại C lại có ${\mathrm{DAB^\backslash widehat\{DAB\}ABC}}^{}=60°$ nên tam giác ABC là tam giác đều.

Vậy tam giác ABC là tam giác đều.