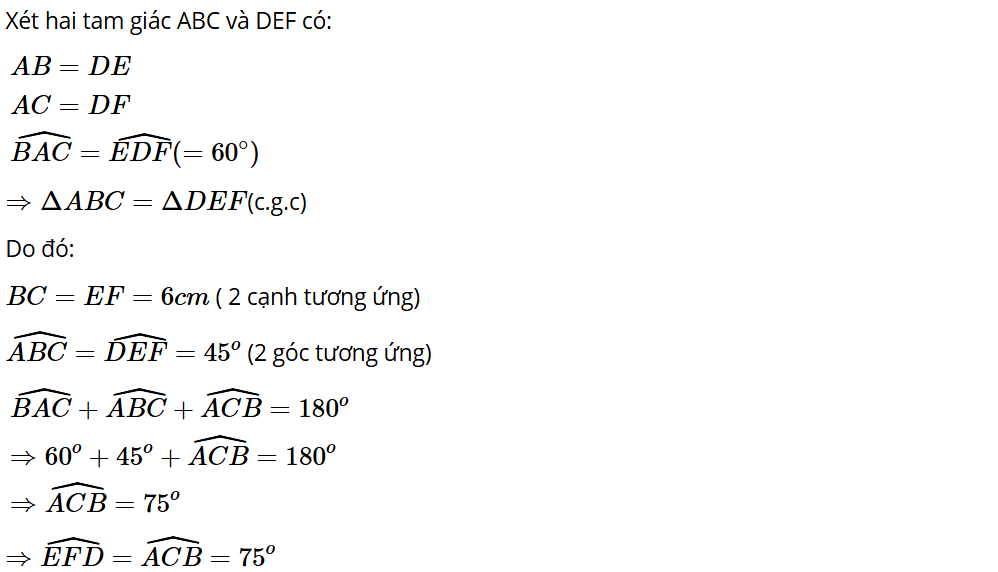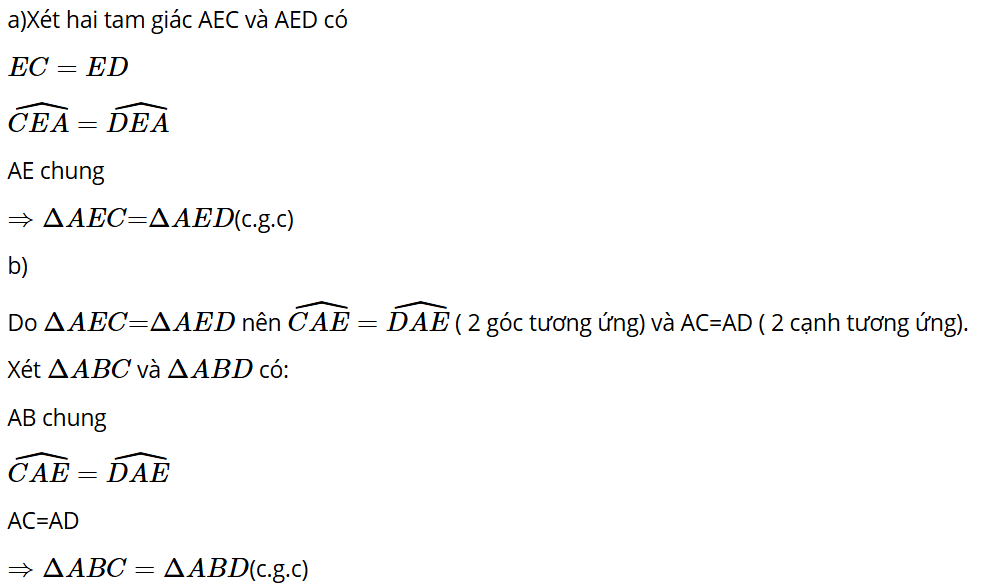Giải SGK Toán 7 Kết nối tri thức Luyện tập chung (trang 74)

Bài 4.16: Cho hai tam giác ABC và DEF thỏa mãn AB = DE, AC = DF,  ${\mathrm{BAC^\backslash widehat\{BAC\}BAC}}^{}={\mathrm{BAC^\backslash widehat\{BAC\}EDF}}^{}=60°,$ BC = 6 cm, ${\mathrm{BAC^\backslash widehat\{BAC\}ABC}}^{}=45°.$ Tính độ dài cạnh EF và số đo các góc ACB, DEF, EFD.

Lời giải:

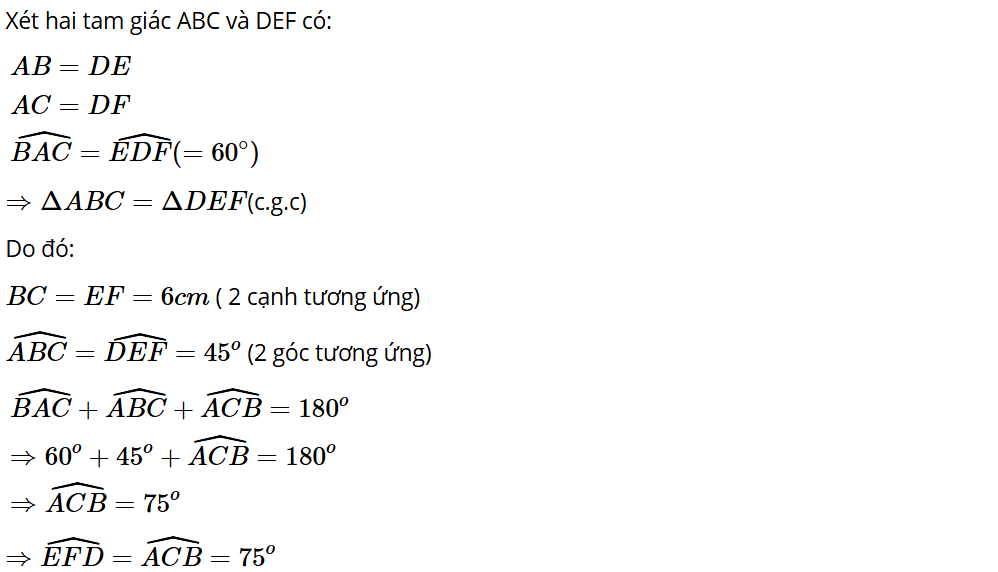
Bài 4.17: Cho hai tam giác ABC và DEF thỏa mãn AB = DE, ${\mathrm{BAC^\backslash widehat\{BAC\}ABC}}^{}={\mathrm{BAC^\backslash widehat\{BAC\}DEF}}^{}=70°,{\mathrm{BAC^\backslash widehat\{BAC\}BAC}}^{}={\mathrm{BAC^\backslash widehat\{BAC\}EDF}}^{}=60°,$ AC = 6 cm. Tính độ dài cạnh DF.

Lời giải:

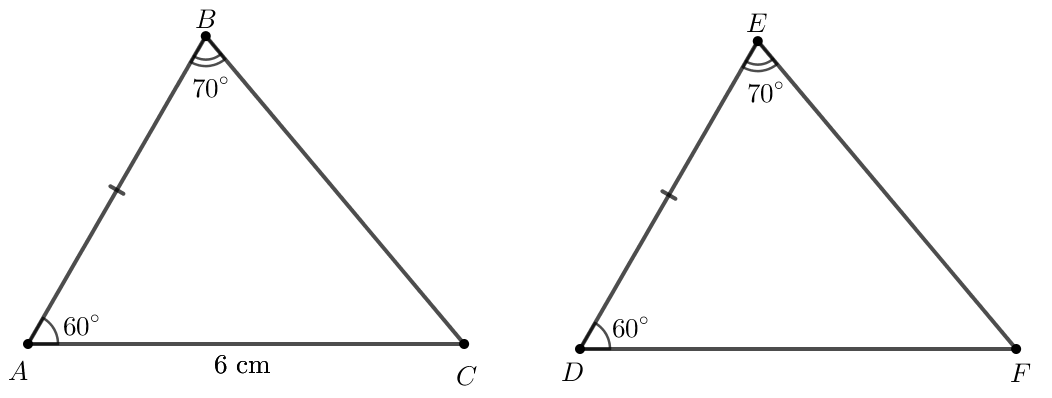
Xét hai tam giác ABC và DEF có:

${\mathrm{BAC^\backslash widehat\{BAC\}ABC}}^{}={\mathrm{BAC^\backslash widehat\{BAC\}DEF}}^{}$ (theo giả thiết).

AB = DE (theo giả thiết).

${\mathrm{BAC^\backslash widehat\{BAC\}BAC}}^{}={\mathrm{BAC^\backslash widehat\{BAC\}EDF}}^{}$ (theo giả thiết).

Vậy $\Delta ABC=\Delta D\text{EF}$ (g – c – g).

Do đó AC = DF = 6 cm (2 cạnh tương ứng).

Vậy DF = 6 cm.

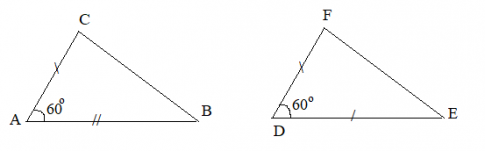
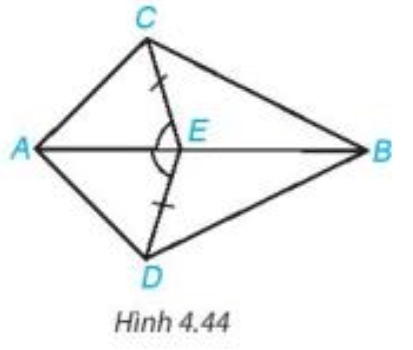
Bài 4.18: Cho Hình 4.44, biết EC = ED và ${\mathrm{BAC^\backslash widehat\{BAC\}AEC}}^{}={\mathrm{BAC^\backslash widehat\{BAC\}AED}}^{}.$ Chứng minh rằng:

a) $\Delta A\text{E}C=\Delta A\text{ED};$

b) $\Delta ABC=\Delta AB\text{D}.$

Lời giải:

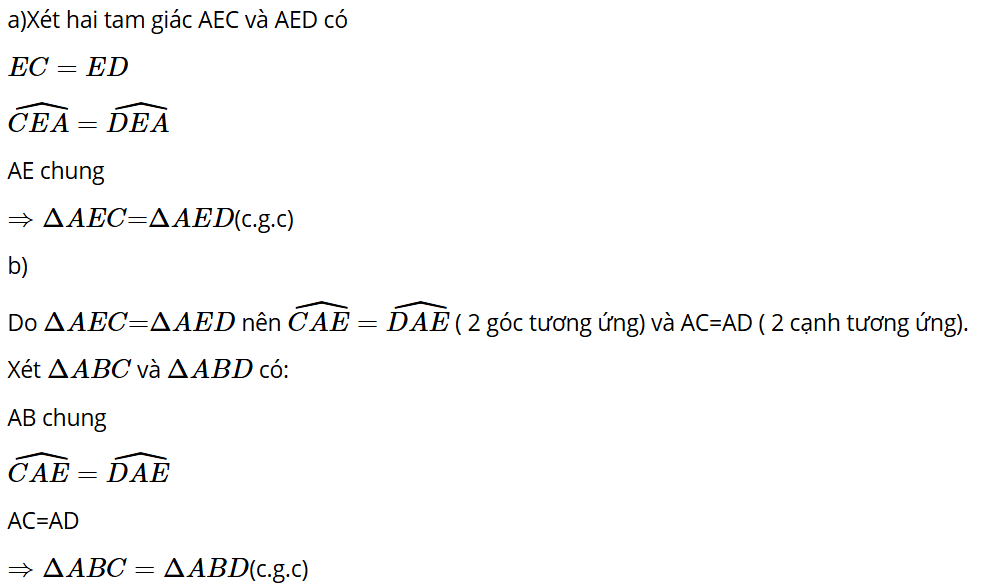
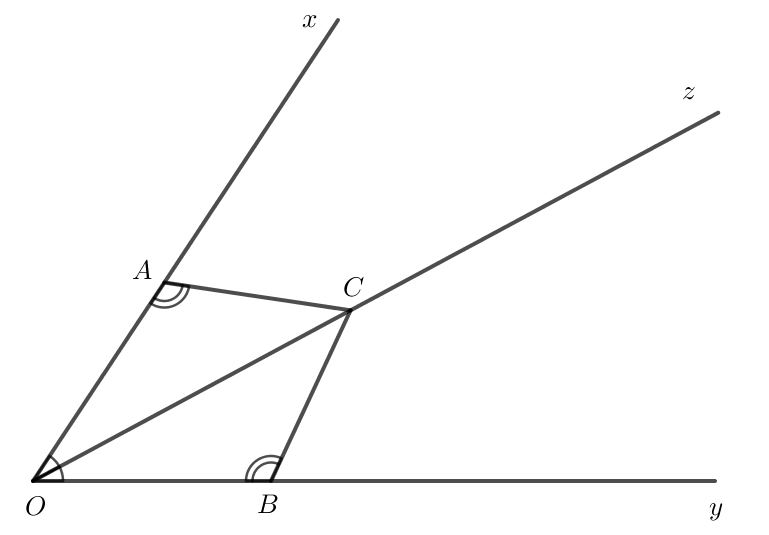
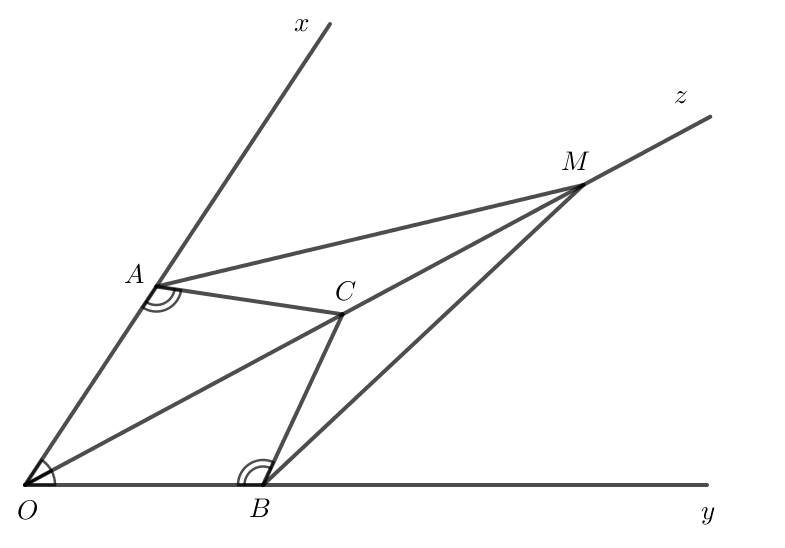
Bài 4.19: Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A, B, C lần lượt thuộc các tia Ox, Oy, Oz sao cho ${\mathrm{CAO^\backslash widehat\{CAO\}CAO}}^{}={\mathrm{CBO^\backslash widehat\{CBO\}CBO}}^{}.$

a) Chứng minh rằng $\Delta OAC=\Delta OBC.$

b) Lấy điểm M trên tia đối của tia CO. Chứng minh rằng $\Delta MAC=\Delta MBC.$

Lời giải:

a)

Do Oz là tia phân giác của góc xOy nên ${\mathrm{AOC^\backslash widehat\{AOC\}AOC}}^{}={\mathrm{BOC^\backslash widehat\{BOC\}BOC}}^{}.$

Xét tam giác OAC có ${\mathrm{AOC^\backslash widehat\{AOC\}AOC}}^{}+{\mathrm{CAO^\backslash widehat\{CAO\}CAO}}^{}+{\mathrm{ACO^\backslash widehat\{ACO\}ACO}}^{}=180°.$

Do đó ${\mathrm{ACO^\backslash widehat\{ACO\}ACO}}^{}=180°-{\mathrm{OC^\backslash widehat\{AOC\}AOC}}^{}-{\mathrm{CAO^\backslash widehat\{CAO\}CAO}}^{}$ (1).

Xét tam giác OBC có ${\mathrm{BOC^\backslash widehat\{BOC\}BOC}}^{}+CBO^\backslash widehat\{CBO\}CBO+{\mathrm{BCO^\backslash widehat\{BCO\}BCO}}^{}=180°.$

Do đó ${\mathrm{BCO^\backslash widehat\{BCO\}BCO}}^{}=180°-{\mathrm{BOC^\backslash widehat\{BOC\}BOC}}^{}-{\mathrm{CBO^\backslash widehat\{CBO\}CBO}}^{}$ (2).

Mà ${\mathrm{AOC^\backslash widehat\{AOC\}AOC}}^{}={\mathrm{BOC^\backslash widehat\{BOC\}BOC}}^{}$ và ${\mathrm{CAO^\backslash widehat\{CAO\}CAO}}^{}=\widehat{CBO}$ nên từ (1) và (2) ta có ${\mathrm{ACO^\backslash widehat\{ACO\}ACO}}^{}={\mathrm{BCO^\backslash widehat\{BCO\}BCO}}^{}.$

Xét hai tam giác OAC và OBC có:

${\mathrm{AOC^\backslash widehat\{AOC\}AOC}}^{}={\mathrm{BOC^\backslash widehat\{BOC\}BOC}}^{}$ (chứng minh trên).

OC chung.

${\mathrm{ACO^\backslash widehat\{ACO\}ACO}}^{}={\mathrm{BCO^\backslash widehat\{BCO\}BCO}}^{}$ (chứng minh trên).

Vậy $\Delta OAC=\Delta OBC$ (g – c – g).

b)

Ta có ${\mathrm{BCM^\backslash widehat\{BCM\}ACM}}^{}$ là góc ngoài tại đỉnh C của tam giác OAC nên ${\mathrm{ACM^\backslash widehat\{ACM\}ACM}}^{}={\mathrm{AOC^\backslash widehat\{AOC\}AOC}}^{}+CAO^\backslash widehat\{CAO\}CAO.$

${\mathrm{BCM^\backslash widehat\{BCM\}BCM}}^{}$ là góc ngoài tại đỉnh C của tam giác OBC nên ${\mathrm{BCM^\backslash widehat\{BCM\}BCM}}^{}=BOC^\backslash widehat\{BOC\}BOC+{\mathrm{CBO^\backslash widehat\{CBO\}CBO}}^{}.$

Mà ${\mathrm{AOC^\backslash widehat\{AOC\}AOC}}^{}={\mathrm{BOC^\backslash widehat\{BOC\}BOC}}^{}$ và ${\mathrm{CAO^\backslash widehat\{CAO\}CAO}}^{}={\mathrm{CBO^\backslash widehat\{CBO\}CBO}}^{}$ nên ${\mathrm{ACM^\backslash widehat\{ACM\}ACM}}^{}={\mathrm{BCM^\backslash widehat\{BCM\}BCM}}^{}.$

Do $\Delta OAC=\Delta OBC$ nên AC = BC (2 cạnh tương ứng).

Xét hai tam giác MAC và MBC có:

AC = BC (chứng minh trên).

${\mathrm{ACM^\backslash widehat\{ACM\}ACM}}^{}={\mathrm{BCM^\backslash widehat\{BCM\}BCM}}^{}$ (chứng minh trên).

MC chung.

Vậy $\Delta MAC=\Delta MBC$ (c – g – c).